A Argentinian old challenge

I found at the Argentinian magazine El Acertijo #17 (1995) the following challenge: 

Definition: A five-line is a piece that results in joining five segments of equal size, aligned consecutively by right angles. There are a total of 23 different five-lines.

The challenge is to use these 23 five-liners to build a perimeter with an area as large as possible, assuming the five-lines are supported by a ground level.

The first example, presented by Héctor San Segundo, the puzzle inventor, had a total area of 491:

In a subsequent number, the best answers to the challenge were presented:

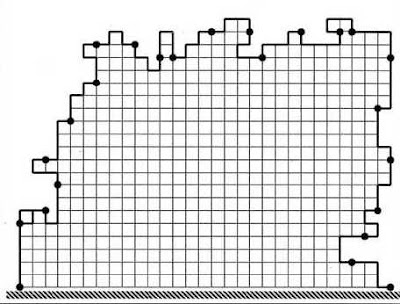
The best result was 793 by Marcelo Iglesias. But Héctor had found a result with 811 units of area (the one shown above).

Afterwards, there was a new record by Pablo Coll with 814 units of area:

He argues, in the text above, that if the perimeter made by the five-liners were able to exactly follow the semi-circle, the maximum area would be around 830 units. So, 814 units is pretty close to that theoretical maximum.

The magazine does not seem to include more information about this puzzle.

Nowadays this problem might be solvable by searching for all valid possibilities. We cannot enumerate and try all solutions (23 factorial is still pretty big) but by searching with some good heuristics, this seems a doable problem.